Introduction

Ge’ez is the ancient language and writing system of the region which makes up northern Ethiopia and Eritrea. It features a unique numeral system which is in use to this day. Ge’ez numerals are used to denote ordinals like calendar years, book chapters, and regnal numbers in much the same way as Roman numerals.

The rules for constructing Ge’ez numerals are inherently recursive, and from those rules a recursive computer algorithm naturally emerges. In this article I formalize a recursive algorithm for converting between Arabic numerals (i.e. conventional base-10 numbers) and Ge’ez numerals.

Compared to iterative methods, a recursive approach is not only much more concise, it’s easier to reason about and verify.

I’ve written a Python implementation of this algorithm as part of Abyssinica, a locale library for the countries of Ethiopia and Eritrea. It’s available on Github and PyPI.

The Ge’ez Numeral System in Brief

Ge’ez has 20 numerical symbols. You’ll notice right away there is no symbol for zero. That’s because the Ge’ez numeral system has no notion of zero, nor any notion of place value. It’s by composing these symbols into sequences representing additions and multiplications that we can represent any positive integer greater than zero.

Arabic to Ge’ez, Case by Case

In this section we describe the recursive function f(n: number) \rightarrow string which takes a number as input and returns its Ge’ez representation.

First we define the helper function f'(n: number) \rightarrow string which simply maps a number to its corresponding Ge’ez symbol.

f'(n) = 
\begin{cases}
፩,& \text{if }n = 1 \\
፪,& \text{if }n = 2 \\
፫,& \text{if }n = 3 \\
\cdots\\
፻,& \text{if }n = 100 \\
፼,& \text{if }n = 10,000 \\
\end{cases}

Case 1: The Number 0 (Base Case)

We take the Ge’ez numeral for n=0 to be the empty string.

f(0) = \epsilon

Case 2: Numbers 1 to 9 (Base Case)

The Ge’ez numeral for n \in [1..9] is simply its corresponding Ge’ez symbol.

f(n) = f'(n)

For example, the Ge’ez numeral for n = 2:

f(2) = f'(2)

Case 3: Numbers 10 to 99

To compute the Ge’ez numeral for n \in [10..99] we first calculate its tens part P = \left\lfloor{n/10}\right\rfloor \cdot 10 and its remainder part Q = n \bmod 10. The Ge’ez numeral for n is given by concatenating the Ge’ez numerals for P and Q like so:

f(n) = f'(P)f(Q)

• Because P \in [10, 20, 30, 40, 50, 60, 70, 80, 90] its Ge’ez numeral is simply its corresponding Ge’ez symbol.
• Because Q \in [0..9] its Ge’ez numeral is computed according to cases 1-2.

For example, the Ge’ez numeral for n = 42:

f(42) = f'(40)f(2)

For Q = 0, f(Q) = \epsilon as given by our first base case. That means when we concatenate f(P) and f(Q), f(Q) is gracefully elided yielding only f(P).

For example, the Ge’ez numeral for n = 40:

\begin{align} 
f(40) &= f'(40)f(0) \\
f(40) &= f'(40) \epsilon\\
f(40) &= f'(40)
\end{align} 

Case 4: Numbers 100 to 199

To compute the Ge’ez numeral for n \in [100..199] we first calculate its remainder part Q = n \bmod 100. The Ge’ez numeral for n is given by concatenating the Ge’ez numerals for 100 and Q like so:

f(n) = f'(100)f(Q)

• Because Q \in [0..99] its Ge’ez numeral is computed according to cases 1-3.

For example, the Ge’ez numeral for n = 142:

f(142) = f'(100)f(42)

Case 5: Numbers 200 to 9,999

To compute the Ge’ez numeral for n \in [200..9,999] we first calculate its hundreds part P = \left \lfloor{n/100}\right \rfloor and its remainder part Q = n \bmod 100. The Ge’ez numeral for n is given by concatenating the Ge’ez numerals for P, 100 and Q like so:

f(n) = f(P)f'(100)f(Q)

• Because P \in [2..99] its Ge’ez numeral is computed according to cases 2-3.
• Because Q \in [0..99] its Ge’ez numeral is computed according to cases 1-3.

For example, the Ge’ez numeral for n = 242:

f(242) = f(2)f'(100)f(42)

Case 6: Numbers 10,000 to 19,999

To compute the Ge’ez numeral for n \in [10,000..19,999) we first calculate its remainder part Q = n \bmod 10,000. The Ge’ez numeral for n is given by concatenating the Ge’ez numerals for 10,000 and Q like so:

f(n) = f'(10,000)f(Q)

• Because Q \in [0..9,999] its Ge’ez numeral is computed according to cases 1-5.

For eample, the Ge’ez numeral for n = 10,242:

f(10,242) = f'(10,000)f(242)

Case 7: Numbers 20,000 to Infinity

To compute the Ge’ez numeral for n \in [20,000..\infty) we first calculate its ten-thousands part P = \left \lfloor{n/10,000}\right \rfloor and its remainder part Q = n \bmod 10,000. The Ge’ez numeral for n is given by concatenating the Ge’ez numerals for P, 10,000 and Q like so:

f(n) = f(P)f'(10,000)f(Q)

• Because P \in [2..\infty) its Ge’ez numeral is computed according to cases 2-7.
• Because Q \in [0..9,999] its Ge’ez numeral is computed according to cases 1-5.

For example, the Ge’ez numeral for n = 20,242:

f(20,242) = f(2)f'(10,000)f(242)

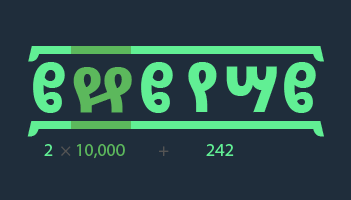
Arabic to Ge’ez in Python

Click here to see arabic_to_geez implemented in Python.

Ge’ez to Arabic, Case by Case

In this section we describe the recursive function g(s: string) \rightarrow number which takes a Ge’ez numeral as input and returns its numeric value.

First we define the helper function g'(s: string) \rightarrow number which simply maps a Ge’ez symbol to its numeric value.

g'(s) = 
\begin{cases}
1,& \text{if }s = ፩ \\
2,& \text{if }s = ፪ \\
3,& \text{if }s = ፫ \\
\cdots\\
100,& \text{if }s = ፻ \\
10\ 000,& \text{if }s = ፼ \\
\end{cases}

Lastly, let s_{Arabic} denote the Arabic representation of the Ge’ez string s .

Case 1: The Empty String (Base Case)

We take the numeric value of the empty string to be 0.

g(\epsilon)=0

Case 2: Ge’ez Numerals 1 to 99 (Base Case)

We know s_{Arabic} \in \{1, 2, 3, ..., 99\} if s doesn’t contain either ፻ or ፼.

To compute the numeric value of s we calculate the arithmetic sum of all the characters in s:

g(s) = \sum\limits_{i} g'(s_{i})

g(፵፪) = 40 + 2

Case 3: Ge’ez Numerals 100 to 9,999

We know s_{Arabic} \in \{100, 101, 102, ..., 9\ 999\} if s contains ፻ and doesn’t contain ፼.

To compute the numeric value of s, we first scan s from the right and split it into strings p, q about the first occurrence of ፻ such that s=p፻q.

The numeric value for s is then given by the following arithmetic expression:

g(s) = max(g(p), 1) \cdot 100 + g(q)

• Because p_{Arabic} \in \{\epsilon, 2, 3, 4, …, 99\} the numeric value of p is computed according to cases 1-2.
• Because q_{Arabic} \in \{\epsilon, 1, 2, 3, …, 99\} the numeric value of q is computed according to cases 1-2 as well.

g(፵፪፻፵፪)=max(g(፵፪), 1) \cdot 100 + g(፵፪)

Case 4: Ge’ez Numerals 10,000 to Infinity

We know s_{Arabic} \in \{10\ 000, 10\ 001, 10\ 002, ...\} if s contains ፼.

To compute the numeric value of s, we first scan s from the right and split it into strings p, q about the first occurrence of ፼ such that s=p፼q.

The numeric value for s is then given by the following arithmetic expression:

g(s) = max(g(p), 1) \cdot 10,000 + g(q)

• Because p_{Arabic} \in \{\epsilon, 2, 3, 4, …\} the numeric value of p is computed according to cases 1-4.
• Because q_{Arabic} \in \{\epsilon, 1, 2, 3, …, 9\ 999\} the numeric value of q is computed according to cases 1-3.

g(፼፵፪፻፵፪) = max(g(\epsilon), 1) \cdot 10,000 + g(፵፪፻፵፪)

Ge’ez to Arabic in Python

Click here to see geez_to_arabic implemented in Python.

Postscript

It’s a great pleasure for me to share this cultural artifact with the world. I hope this article contributes towards the preservation and study of Ge’ez for future generations.